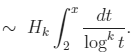
|
|
© 2011 by Alexei Kourbatov, JavaScripter.net/math
Main article: Maximal gaps between prime k-tuples
The
Hardy-Littlewood k-tuple conjecture
allows one to predict the average frequencies of prime k-tuples near p,
as well as the approximate total counts of prime k-tuples below x.
Specifically, the Hardy-Littlewood k-tuple constants
Frequency of k-tuples ≈ Hk / logkp or, equivalently, Total number of k-tuples below x 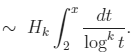
Reciprocal Hardy-Littlewood constants multiplied by logkp determine the average gap between prime k-tuples near p:
Expected average gap a = Ck logkp, where Ck = 1/Hk.
Using the expected average gap a, we can estimate maximal gaps gk between prime k-tuples near p:
Expected maximal gap = a(log(p/a) − b), with a = Ck logkp, b ≈ 2/k .
Table. Hardy-Littlewood constants for prime k-tuples up to k = 8.
| Name of prime k-tuple | Width | Pattern | Hardy-Littlewood constant Hk |
Reciprocal |
|---|---|---|---|---|
| 2-tuple, twin primes, twins | 2 | 0 2 | 1.32032 | 0.757392 |
| 3-tuple, triplet (type A) | 6 | 0 4 6 | 2.85825 | 0.349864 |
| 3-tuple, triplet (type B) | 6 | 0 2 6 | 2.85825 | 0.349864 |
| 4-tuple, quadruplet | 8 | 0 2 6 8 | 4.15118 | 0.240895 |
| 5-tuple, quintuplet (type A) | 12 | 0 4 6 10 12 | 10.13179 | 0.09869924 |
| 5-tuple, quintuplet (type B) | 12 | 0 2 6 8 12 | 10.13179 | 0.09869924 |
| 6-tuple, sextuplet | 16 | 0 4 6 10 12 16 | 17.29861 | 0.05780811 |
| 7-tuple, septuplet (type A) | 20 | 0 2 6 8 12 18 20 | 53.97195 | 0.01852814 |
| 7-tuple, septuplet (type B) | 20 | 0 2 8 12 14 18 20 | 53.97195 | 0.01852814 |
| 8-tuple, octuplet (type A) | 26 | 0 2 6 8 12 18 20 26 | 178.26195 | 0.005609722 |
| 8-tuple, octuplet (type B) | 26 | 0 6 8 14 18 20 24 26 | 178.26195 | 0.005609722 |
| 8-tuple, octuplet (type C) | 26 | 0 2 6 12 14 20 24 26 | 475.36521 | 0.002103646 |
Hardy-Littlewood constants can be computed with a high precision; see Tony Forbes k-tuplets pages for more information on this.
Copyright © 2011, Alexei Kourbatov, JavaScripter.net.